2.10.2 Unary operators
Unary operators have one operand, but three notations: prefix, postfix and bifix. With the first two notations, an operator symbol comes before or after the operand. With bifix notation, the operand comes between two operator symbols. Figure 2.53 summarizes the unary operators. Operands of unary operators can be complex expressions whose expression type is one of real, complex, radial, vector, tuple, set or matrix.
| Name | Symbol | Notation | Result | . | ⅈ | ɽ | ƈ | ʋ | ʂ | ʈ | ɱ | ɗ | |
| Angle | ∠ | prefix | . | ✓ | ✓ | ✓ | |||||||
| Cardinality | # | prefix | . | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Cardinality | ## | prefix | . | ✓ | |||||||||
| Cast | . ⅈ ɽ ƈ ʋ ʈ ʂ ɱ | postfix | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| Ceiling | ⌈ and ⌉ | bifix | o | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| Cofactor | C | postfix | ɱ | ✓ | |||||||||
| Complement | ¬ | prefix | o | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| Conjugate | ¬ | prefix | ⅈ | ✓ | |||||||||
| Degree | ° | postfix | . | ✓ | |||||||||
| Determinant | D | postfix | . | ✓ | |||||||||
| Factorial | ! | postfix | . | ✓ | |||||||||
| Floor | ⌊ and ⌋ | bifix | o | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| Gauss | G | postfix | m | ✓ | |||||||||
| Identity | + | prefix | o | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Inverse | ^-1 | postfix | ɱ | ✓ | |||||||||
| Jordan | J | postfix | m | ✓ | |||||||||
| Magnitude | | and | | bifix | o | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Max | ⌈ and ⌉ | bifix | o | ✓ | ✓ | ✓ | |||||||
| Min | ⌊ and ⌋ | bifix | o | ✓ | ✓ | ✓ | |||||||
| Nabla | ∇ | prefix | ʋ | ✓ | |||||||||
| Negation | - | prefix | . | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Parametric | P | postfix | t | ✓ | |||||||||
| Partition | ↑, ↓ | prefix | o | ✓ | ✓ | ✓ | |||||||
| Plus or Minus | ± | prefix | o | ✓ | ✓ | ✓ | |||||||
| Precedence | ( and ) | bifix | o | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Sqrt | √ | prefix | . | ✓ | |||||||||
| Transcendentals | sin, etc. | prefix | . | ✓ | |||||||||
| Transpose | T | postfix | ƈʋɱɱ | ✓ | ✓ | ✓ | ✓ |
Angle
extracts the angle from a radial value. If applied to a vector, this operator converts the vector to a radial value and extracts the angle.
The angle operator can be decorated with an integer non-negative subscript to extract other than the first angle from multi-dimensional vectors.
For example, if 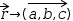
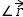

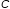
Cardinality produces the number of items in a collection. The cardinality of a generator produces a real value only if the generator is iterable.
There are some special cases. The cardinality of a real is always 0. The number of columns in a matrix
can be found using the ## form of the operator. Examples: 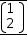

Cast changes the type of an expression and converts its operand (the source) to a value (the destination) compatible with the type specified by the cast operator (the destination type). For composite and collection operands, the source supplies a sequence of expressions which are imported into the destination value. For composite destination types, the source must supply a sequence of scalars; this is implied for composites and conditional for collections. If the source is a radial, it is first converted to a vector using the magnitude and angle(s).
If the destination is a radial, the sequence is converted to magnitude and angle(s). Conversion to radial only works for sequences of 2 or 3 expressions.
If the source is a matrix, it can be reshaped by casting it to a tuple and using the ↑ operator; 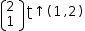
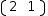
If the destination is a string, the parsable representation of the source is produced as the value of the string. If the source is a string, it is parsed and the resulting expression is cast to the destination type.
Ceiling. For real operands, finds the nearest integer that is larger than its non-integer operand. For collections, extracts the real with maximum value. For vectors, applies the ceiling operator to each element. Does not apply to complex and radial values, but can be restructured across components of such values.
Cofactor produces the cofactor matrix for a matrix.
Complement changes the value of its operand in the Boolean sense: zero becomes 1 and all other values become zero. The result is displayed as Boolean.
Conjugate restructures a complex number by negating the imaginary part.
Degree converts a real value to radians.
Determinant restructures a square matrix into a real expression representing the determinant of the matrix.
Factorial summarizes a product of integers.
Floor. For real operands, finds the nearest integer that is smaller than its non-integer operands. For collections, extracts the real with minimum value. For vectors, applies the floor operator to each element.
Gauss performs Gaussian elimination on a matrix leaving it in row-echelon form. See also Jordan.
Identity leaves its operand unchanged in sign. Provided for completeness, for use where positivity must be emphasized in contrast to negation.
Inverse inverts a matrix. The matrix must be iterable and contain evaluable items.
Magnitude Finds the magnitude of a value using the Pythagorean rule. Does not apply to matrices.
Jordan performs Gauss-Jordan elimination on a matrix leaving it in reduced-echelon form. See also Gauss.
Max finds the maximum value in a collection. The input form allows a closing parenthesis in place of a closing half-bracket.
Min finds the minimum value in a collection. The input form allows a closing parenthesis in place of a closing half-bracket.
Nabla creates a vector of partial derivatives from a multi-variable real expression.
Negation
changes the sign of a value so that, for example, 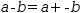
Not
changes a Boolean value so 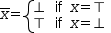
Plus or Minus provides a shorthand notation for a set of two real values, each the same in magnitude and opposite in sign.
Parametric transforms a matrix to row-echelon form and then transforms the result to a tuple of vectors representing the solution to a system of linear equations in parametric form.
Partition operators ↑ and ↓ behave like their binary counterparts with the right operand
implied to be 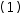
Precedence causes the operators that make up the operand to bind more closely than the operators of which the precedence operator is an operand.
Square Root
provides a short hand notation for binary 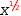
Transcendentals. The transcendental natural log (ln), base-10 log (log), trigonometric and inverse trigonometric functions are written as prefix unary operators.
Transpose restructures a matrix by exchanging rows or columns. Restructures a tuple by using its items to create a column matrix. The matrix or tuple must be iterable. Transpose also converts between row and column vectors.